Numerical Aperture
Numerical Aperture (also termed Object-Side Aperture) is a value (often symbolized by the abbreviation NA) originally defined by Abbe for microscope objectives and condensers. It is given by the simple expression:
Formula 1 - Numerical Aperture
$$\textrm{Numerical Aperture (NA)} = n \times \sin(µ) \ \textrm{or} \ n \times \sin(α)$$Note: Many authors use the variable µ to designate the one-half angular aperture while others employ the more common term α, and in some instances, θ.
In the numerical aperture equation, n represents the refractive index of the medium between the objective front lens and the specimen, and µ or α is the one-half angular aperture of the objective.
Figure 1 - Numerical Aperture
The numerical aperture of a microscope objective is a measure of its ability to gather light and resolve fine specimen detail at a fixed object distance. Image-forming light waves pass through the specimen and enter the objective in an inverted cone as illustrated in Figure 1 (above). A longitudinal slice of this cone of light reveals the angular aperture, a value that is determined by the focal length of the objective.
Interactive Tutorial - Numerical Aperture Light Cones
Numerical aperture is a measure of the highly diffracted light rays captured by the objective.
In practice, it is difficult to achieve numerical aperture values above 0.95 with dry objectives. Figure 1 illustrates a series of light cones derived from objectives of varying focal length and numerical aperture. As the light cones grow larger, the angular aperture (α) increases from 7° to 60°, with a resulting increase in the numerical aperture from 0.12 to 0.87, nearing the limit when air is utilized as the imaging medium. Higher numerical apertures can be obtained by increasing the imaging medium refractive index (n) between the specimen and the objective front lens. Microscope objectives are now available that allow imaging in alternative media such as water (refractive index = 1.33), glycerin (refractive index = 1.47), and immersion oil (refractive index = 1.51). The numerical aperture of an objective is also dependent, to a certain degree, upon the amount of correction for optical aberration.
Figure 2 - Numerical Aperture versus Objective Magnification
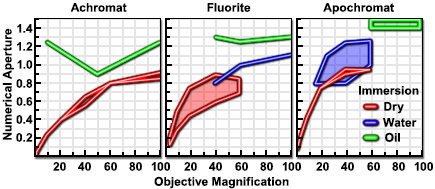
Highly corrected objectives tend to have much larger numerical apertures for the respective magnification as illustrated in Figure 2 and Table 1 below. If we take a series of typical 10x objectives as an example, we see that for flat-field corrected plan objectives, numerical aperture increases correspond to enhanced correction for chromatic and spherical aberration: plan achromat, N.A. = 0.25; plan fluorite, N.A. = 0.30; and plan apochromat, N.A. = 0.45.
This feature of increasing numerical aperture across an increasing optical correction factor in a series of objectives of similar magnification holds true throughout the range of magnifications as shown in Table 1. Most manufacturers strive to ensure that their objectives have the highest correction and numerical aperture that is possible for each class of objective.
Table 1 - Numerical Aperture versus Optical Correction
| Magnification | Plan Achromat (NA) | Plan Fluorite (NA) | Plan Apochromat (NA) |
|---|---|---|---|
| 0.5x | 0.025 | n/a | n/a |
| 1x | 0.04 | n/a | n/a |
| 2x | 0.06 | n/a | 0.10 |
| 4x | 0.10 | 0.13 | 0.20 |
| 10x | 0.25 | 0.30 | 0.45 |
| 20x | 0.40 | 0.50 | 0.75 |
| 40x | 0.65 | 0.75 | 0.95 |
| 40x (oil) | n/a | 1.30 | 1.00 |
| 60x | 0.75 | 0.85 | 0.95 |
| 60x (oil) | n/a | n/a | 1.40 |
| 100x (oil) | 1.25 | 1.30 | 1.40 |
| 150x | n/a | n/a | 0.90 |
A majority of objectives in the magnification range between 60x and 100x (and higher) are designed for use with immersion oil. By examining the numerical aperture equation presented above, we find that the highest theoretical numerical aperture obtainable with common immersion oils is 1.51 (when sin (α) = 1). In practice, however, most oil immersion objectives have a maximum numerical aperture of 1.4, with the most common numerical apertures ranging from 1.0 to 1.35.
Note: Unless specified by image-side, the term numerical aperture refers to the object side.
Contributing Author
Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.
















